Markus−Yamabe conjecture
In mathematics, the Markus-Yamabe conjecture is a conjecture on global asymptotic stability. The conjecture states that if a continuously differentiable map on an  -dimensional real vector space has a single fixed point, and its Jacobian matrix is everywhere Hurwitz, then the fixed point is globally stable.
-dimensional real vector space has a single fixed point, and its Jacobian matrix is everywhere Hurwitz, then the fixed point is globally stable.
The conjecture is true for the two-dimensional case. However, counterexamples have been constructed in higher dimensions. Hence, in the two-dimensional case only, it can also be referred to as the Markus-Yamabe theorem.
Related mathematical results concerning global asymptotic stability, which are applicable in dimensions higher than two, include various autonomous convergence theorems. A modified version of the Markus-Yamabe conjecture has been proposed, but at present this new conjecture remains unproven.[1]
Mathematical statement of conjecture
- Let
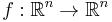 be a
be a 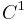 map with
map with 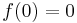 and Jacobian
and Jacobian 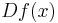 which is Hurwitz stable for every
which is Hurwitz stable for every 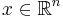 .
.
- Then
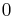 is a global attractor of the dynamical system
is a global attractor of the dynamical system 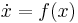 .
.
The conjecture is true for 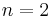 and false in general for
and false in general for 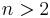 .
.
Notes
References
- L. Markus and H. Yamabe, "Global Stability Criteria for Differential Systems", Osaka Math J. 12:305-317 (1960)
- Gary Meisters, A Biography of the Markus-Yamabe Conjecture (1996)
- C. Gutierrez, "A solution to the bidimensional Global Asymptotic Stability Conjecture", Ann. Inst. H. Poincaré Anal. Non Linéaire 12: 627–671 (1995).
- R. Feßler, "A proof of the two-dimensional Markus-Yamabe stability conjecture and a generalisation", Ann. Polon. Math. 62:45-47 (1995)
- A. Cima et al., "A Polynomial Counterexample to the Markus-Yamabe Conjecture", Advances in Mathematics 131(2):453-457 (1997)
- Josep Bernat and Jaume Llibre, "Counterexample to Kalman and Markus-Yamabe Conjectures in dimension larger than 3", Dynam. Contin. Discrete Impuls. Systems 2(3):337-379, (1996)